今回取り扱う問題は2023年大阪大学の文系で出題された問題です。
対数が絡んだ問題ですが、微分の力が試される問題です。
文字の値によって、最大値・最小値を取る値が変わるような問題で、微分が得意な人と苦手な人で差がつきます。
微分を勉強中の人、微分に強くなりたい人、受験生はぜひ最後までお読みください。
それではさっそくやっていきましょう。
勉強おすすめアイテム
問題文
$y=\big (\log_{\frac{1}{2}}x\big )^3+a\big (\log_{\sqrt{2}}x\big )\big (\log_{4}x^3\big )$
とする。
(1)$t=\log_{2}x\,$とするとき,$y\,$を$\,a,\, t\,$を用いて表せ。
(2)$x\,$が$\dfrac{1}{2}\leqq x\leqq 8\,$の範囲を動くとき,$y\,$の最大値$\, M\,$を$\, a\,$を用いて表せ。
自力で解いてみたい方は、ここでいったんストップして挑戦してみてください。
動画で解説を見たい方へ
YouTubeでも本問題を解説しています。
動画での解説は下記より確認できます。
YouTubeでも数学・算数の良問や難問を解説しています。
良かったらチャンネル登録お願いします。 チャンネル登録はこちら
本問題を解く上での考え方・ポイント
(1)の誘導がなくても、解けるようになりたい問題です。
(1)は底が$\,\frac{1}{2},\sqrt{2},4\,$ということなので、見た瞬間に底を$\, 2\,$で揃えたいと考えたいです。
(1)は丁寧に$\,t=\log_{2}x\,$と与えてくれています。対数の底の変換公式を用いて、底を$\, 2\,$で揃えましょう。
本問題の差がつくのは(2)です。
(1)で求めた結果、$y\,$は$\, t\,$の3次関数で表すことができます。また、$x\,$が$\dfrac{1}{2}\leqq x\leqq 8\,$ということで、$-1\leqq t\leqq 3$です。
この範囲で最大値を考えるということで、微分していくのですが、$y’=0\,$となる$\, t\,$は$\,t=0,\, 2a\,$と分かります。
この$\,2a\,$の値によって、増減表は変わってくるので場合分けする必要があります。
($2a\,$が3以上のときと3未満のときの2つで場合分けします。)
(ざっくりとした増減表ですが、以下の2つで場合分けする必要があります。)
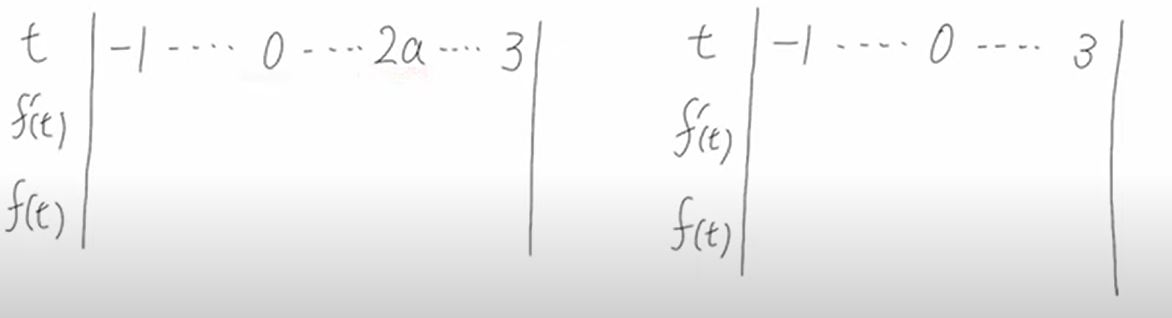
また、最大値を取る候補が複数出るので、どちらが最大になるかをきちんと考える必要もあります。
解答・解説
では、上記のポイントを抑えたところで解答です。
(1)の解答
$y=\big (\log_{\frac{1}{2}}x\big )^3+a\big (\log_{\sqrt{2}}x\big )\big (\log_{4}x^3\big )$
$\quad =\Big (\dfrac{\log_2 x}{\log_2 \frac{1}{2}}\Big )^3 + a\Big (\dfrac{\log_2 x}{\log_2 \sqrt{2}}\Big )\Big (\dfrac{\log_2 x^3}{\log_2 4}\Big )$
$\quad =(-\log_2 x)^3 + a\Big (\dfrac{\log_2 x}{\frac{1}{2}}\Big )\Big (\dfrac{3\log_2 x}{2}\Big )$
$\quad = -t^3+3at^2$
(2)の解答
$f(t)=-t^3+3at^2\,$とおく。
$x\,$が$\dfrac{1}{2}\leqq x\leqq 8\,$であるから、$\log_2 \dfrac{1}{2}\leqq \log_2 x\leqq \log_2 8$である。
$\therefore \, -1\leqq t\leqq 3$
$f'(t)=-3t^2+6at$
$\quad = -3t(t-2a)$
$\therefore \, f'(t)=0\,$のとき,$t=0,\, 2a$
(ⅰ)$0<2a<3\,$すなわち、$0<a<\frac{3}{2}\,$のとき、
増減表は下記。
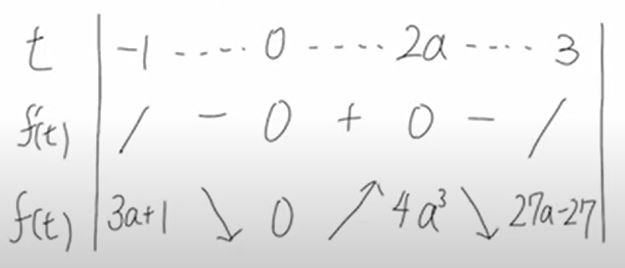
最大値となり得るのは、$f(-1)=3a+1\,$、もしくは$f(2a)=4a^3\,$である。
$4a^3\,$と$\,3a+1\,$の大小関係について考える。
$4a^3-(3a+1)$
$=(a-1)(4a^2+4a+1)$
$=(a-1)(2a+1)^2$
$a\,$は正の実数より、$(2a+1)^2>0$
$\therefore \,$ $0<a<1\,$のとき、$4a^3<3a+1$
$1\leqq a<\frac{3}{2}\,$のとき、$4a^3\geqq 3a+1$
以上より、
$0<a<1\,$のとき、$M=f(-1)=3a+1$
$1\leqq a<\frac{3}{2}\,$のとき、$M=f(2a)=4a^3$
(ⅱ)$2a\geqq 3\,$すなわち、$a\geqq \frac{3}{2}\,$のとき、
増減表は下記。
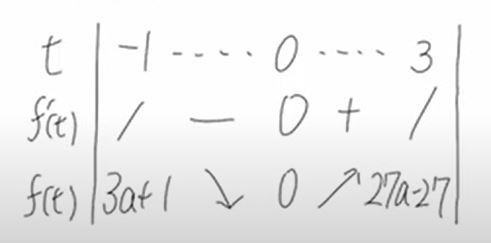
$3a+1\,$と$\,27a-27\,$の大小関係について考える。
$(27a-27)-(3a+1)$
$=24a-28$
$\geqq 24\cdot\frac{3}{2} -28$
$=8>0$
$\therefore \,$ $a\geqq \frac{3}{2}\,$において、$27a-27>3a+1$
$\therefore \,$ $M=f(3)=27a-27$
(ⅰ)(ⅱ)より、求める$\,M\,$は
$3a+1(0<a<1)$
$4a^3(1\leqq a<\frac{3}{2})$
$27a-27(a\geqq \frac{3}{2})$
受験勉強・予習復習にはスタサプ
自宅でトップ講師による授業を受けることができるスタサプ。
予備校に通わなくても、スマホで自分のレベルに合わせて授業を受けることができます。
6教科19科目に対応。共通テスト対策講座や志望校別対策講座も全て見放題です。
(僕も数学の学び直しで活用していますが、控えめに言って最高です)
無料体験もあるので、本気で成績を伸ばしたい人はぜひ。
※無料体験はいつ終わるか分からないのでお早めに
さいごに
いかがでしたでしょうか。
今回は2023年大阪大学の対数×微分の問題を解説しました。
文字が取り得る値の範囲をしっかりと考え、文字の値によって最大値・最小値を取る場所が変わるような問題は頻出で差がつくので、しっかりと解けるようになっておきましょう。
また、数学の成績を伸ばしたいと考えている方向けにおすすめの数学の参考書を下記でまとめています。

参考書はとにかく自分に合ったレベルのものを1冊やり切ることがとにかく重要です。
レベルに応じた参考書をやり切る→数学力が向上→レベルに応じた参考書をやり切る→・・・と取り組んでいくことで力がつきます。
参考になれば幸いです。





