今回取り扱う問題は2023年京都大学の問題です。
三角関数の問題で$72^\circ$を扱っていくような問題です。$18^\circ \times $(整数)の角を扱う問題の解法は基本的に決まっているのでしっかりと取りたい問題でした。
それではさっそくやっていきましょう。
勉強おすすめアイテム
問題文
(2) 半径$\,1\,$の円に内接する正五角形の一辺の長さが$\,1.15\,$より大きいか否かを理由を付けて判定せよ。
これから先は解説になります。
自力で解いてみたい方は、ここでいったんストップして挑戦してみてください。
動画で解説を見たい方へ
YouTubeでも本問題を解説しています。
動画での解説は下記より確認できます。
YouTubeでも数学・算数の良問や難問を解説しています。
良かったらチャンネルしてもらえると嬉しいです。
本問題を解く上での考え方・ポイント
(1)の考え方・ポイント
2倍角と3倍角の公式の確認問題です。
覚えている人は一発ですが、覚えていない人は自分で導くことになります。三角関数の公式は覚えている人も覚えていない人も自分で導けるようになっておくべきです。
三角関数の公式はすべて加法定理から導くことができるので、しっかりと導けるようになっておきましょう。
(2)の考え方・ポイント
正五角形の１辺の長さを考えていきたいので、余弦定理を使って一辺の長さを考えていきます。
円の中心と正五角形の頂点を結ぶと三角形ができるので、その三角形で余弦定理を用いていきます。
そこで問題となってくるのが、$\cos 72^\circ\,$の値です。
（１）で誘導があるので思いつきやすいですが、$18^\circ\times$(整数)の角度は5倍することで扱いやすい角度になってくれます。
なので、$5\theta\,$を考えていくことになるのですが、$5\theta = 2\theta + 3\theta$とすることで、2倍角の公式や3倍角の公式まで落とし込むことができます。
解答・解説
(1)の解答
$\cos 2\theta$
$=\cos (\theta + \theta )$
$=\cos\theta\cos\theta – \sin\theta\sin\theta$
$=\cos ^2\theta – \sin ^2 \theta$
$=\cos ^2\theta – (1-\cos ^2\theta)$
$=2\cos ^2\theta -1$
$\cos 3\theta$
$=\cos (2\theta +\theta)$
$=\cos 2\theta\cos\theta – \sin 2\theta\sin\theta$
$=(2\cos ^2\theta -1)\cos\theta -2\sin ^2\theta\cos\theta$
$=2\cos ^3\theta – \cos\theta -2(1- \cos ^2\theta )\cos\theta$
$=4\cos ^3\theta -3\cos\theta$
(2)の解答
下記の図について考える。
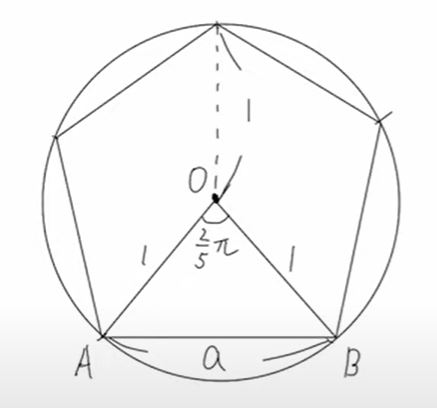
$AB=a\,$として、$\triangle OAB\,$において余弦定理より、
$a^2 = 1^2 +1^2-2\cdot 1\cdot 1\cdot \cos\dfrac{2}{5}\pi $
$\; =2-2\cos\dfrac{2}{5}\pi\cdots ①$
$\theta = \dfrac{2}{5}\pi\,$とすると、
$5\theta = 2\pi\,$
$\Leftrightarrow 3\theta +2\theta =2\pi$
$\Leftrightarrow 3\theta = 2\pi – 2\theta$
$\therefore \, \cos 3\theta = \cos (2\pi -2\theta )$であるから、
$\cos 3\theta = \cos 2\theta$
(1)より
$4\cos ^3\theta -3\cos\theta = 2\cos ^2\theta -1$
$\Leftrightarrow 4\cos ^3\theta-2\cos ^2\theta -3\cos \theta+1=0$
$\Leftrightarrow (\cos\theta -1)(4\cos ^2\theta +2\cos\theta -1)=0$
$\theta = \dfrac{2}{5}\pi\,$であるから、$0<\cos\theta <1$
$\therefore \,\cos\theta = \dfrac{-1+\sqrt{5}}{4}$
①に代入すると
$a^2 = 2-2\cdot\dfrac{-1+\sqrt{5}}{4}$
$\;=\dfrac{5-\sqrt{5}}{2}$
$a^2-(1.15)^2$について考える。
$2.2<\sqrt{5}<2.3\,$より、
$\dfrac{5-2.3}{2}-1.3225<\dfrac{5-\sqrt{5}}{2}-1.3225 <\dfrac{5-2.2}{2}-1.3225$
$\therefore \, a^2>(1.15)^2\,$であるから、$a>1.15$ $(\because \,a>0)$
$\therefore \,$ 1辺の長さは$\,1.15\,$よりも大きい。
受験勉強・予習復習にはスタサプ
自宅でトップ講師による授業を受けることができるスタサプ。
予備校に通わなくても、スマホで自分のレベルに合わせて授業を受けることができます。
6教科19科目に対応。共通テスト対策講座や志望校別対策講座も全て見放題です。
（僕も数学の学び直しで活用していますが、控えめに言って最高です）
無料体験もあるので、本気で成績を伸ばしたい人はぜひ。
※無料体験はいつ終わるか分からないのでお早めに
さいごに
いかがでしたでしょうか。
今回は2023年京都大学の問題を解説しました。
$18^\circ\times$(整数) の形は頻出なのでしっかりと解けるようになっておきましょう。
また、数学の成績を伸ばしたいと考えている方向けにおすすめの数学の参考書を下記でまとめています。
参考書はとにかく自分に合ったレベルのものを１冊やり切ることがとにかく重要です。
レベルに応じた参考書をやり切る→数学力が向上→レベルに応じた参考書をやり切る→・・・と取り組んでいくことで力がつきます。
レベル別におすすめの参考書をまとめているので、参考書・問題集選びの参考にしてもらえれば幸いです。
今回は以上です。
受験勉強・予習復習にはスタサプ
自宅でトップ講師による授業を受けることができるスタサプ。
予備校に通わなくても、スマホで自分のレベルに合わせて授業を受けることができます。
6教科19科目に対応。共通テスト対策講座や志望校別対策講座も全て見放題です。
（僕も数学の学び直しで活用していますが、控えめに言って最高です）
無料体験もあるので、本気で成績を伸ばしたい人はぜひ。
※無料体験はいつ終わるか分からないのでお早めに
