今回取り扱う問題は2014年京都大学の理系で出題された問題です。
面積の最大を求めるような問題で、問題文から式を考えて微分して最大値を求めるような頻出の問題です。
それではさっそくやっていきましょう。
問題文
このとき，$\cos\angle B\,$を求めよ。
これから先は解説になります。
自力で解いてみたい方は、ここでいったんストップして挑戦してみてください。
動画で解説を見たい方へ
YouTubeでも本問題を解説しています。
動画での解説は下記より確認できます。
YouTubeでも数学・算数の良問や難問を解説しています。
良かったらチャンネル登録お願いします。 チャンネル登録はこちら
本問題を解く上での考え方・ポイント
$\angle B=2\angle A\,$という条件から、$\angle A = \theta\,$と置くことで、$\angle B = 2\theta\,$と表すことができ、本問題を考えやすくなります。
どの問題でも共通して言える大事なことですが、自分で文字を置いたら、その文字が取り得る値の範囲をきちんと考える癖をつけておきましょう。
今回で言うと、図形$\triangle ABC$に着目して、三角形であるための条件から$\theta\,$の取り得る値の範囲を考えましょう。
$\angle A = \theta,\, \angle B = 2\theta\,$であるから、残った$\angle C$は、$\angle C = \pi – 3\theta\,$と表すことができます。
これら全ての角は$0$より大きく、$\pi\,$より小さい必要があります。
あとは、$\triangle ABC\,$を$\theta\,$の式で表して、微分して最大のときを考えていけば解けそうです。
受験勉強・予習復習にはスタサプ
自宅でトップ講師による授業を受けることができるスタサプ。
予備校に通わなくても、スマホで自分のレベルに合わせて授業を受けることができます。
6教科19科目に対応。共通テスト対策講座や志望校別対策講座も全て見放題です。
（僕も数学の学び直しで活用していますが、控えめに言って最高です）
無料体験もあるので、本気で成績を伸ばしたい人はぜひ。
※無料体験はいつ終わるか分からないのでお早めに
解答・解説
解説
本問題を解くうえで正弦定理や積和の公式などを利用します。
三角関数の倍角の公式や積和の公式など、公式が覚えられないという人が多いですが、それらは全て加法定理から簡単に導くことができます。いつでも自分ですぐに導けるようにしておきましょう。
ということで、本問題のポイントを踏まえたうえで解答になります。
解答
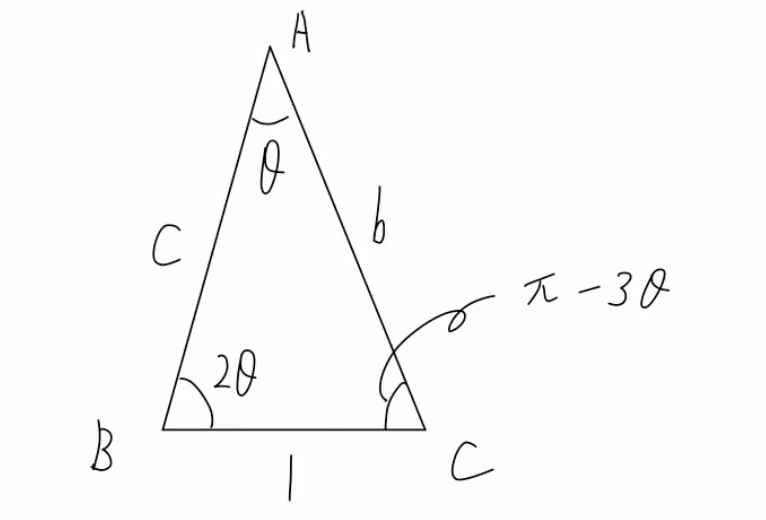
上の図で考える。
$\angle C = \pi -3\theta$であり、
$0<\theta < \pi,\, 0<2\theta < \pi ,\, 0<\pi – 3\theta < \pi\,$より、
$0<\theta < \dfrac{\pi}{3}\,$である。$\cdots$①
$\triangle ABC$の面積を$S\,$とすると、
$S=\dfrac{1}{2} \cdot 1 \cdot c \cdot \sin 2\theta\,\cdots$②
と表せる。
また、$\triangle ABC$において正弦定理より、
$\dfrac{1}{\sin\theta}=\dfrac{b}{\sin 2\theta}=\dfrac{c}{\sin (\pi – 3\theta)}$
$\therefore \,$ $c=\dfrac{\sin 3 \theta}{\sin\theta}$ $(\because \,\sin (\pi -3\theta )=\sin 3\theta)$
これを②に代入すると、
$S=\dfrac{1}{2}\cdot\dfrac{\sin 3\theta}{\sin\theta}\cdot\sin 2\theta$
$\quad =\dfrac{1}{2}\cdot\dfrac{\sin 3\theta}{\sin\theta}\cdot 2\sin\theta\cos\theta$
$\quad =\sin 3\theta\cos\theta$
$\quad =\dfrac{1}{2}(\sin 4\theta + \sin 2\theta)$
$f(\theta )=\dfrac{1}{2}(\sin 4\theta + \sin 2\theta)$ とおく。$(0<\theta < \dfrac{\pi}{3})$
$f'(\theta )=\dfrac{1}{2}(4\cos 4\theta + 2\cos 2\theta)$
$\qquad = 2\cos 4\theta + \cos 2\theta$
$f'(\theta )=0$のときを考える。
$2\cos 4\theta + \cos 2\theta$
$=2(2\cos ^2 2\theta -1)+\cos 2\theta$
$=4\cos ^2 2\theta + \cos 2\theta -2 = 0$
$\therefore \, \cos 2\theta = \dfrac{-1+\sqrt{33}}{8}$ $(\because \, 0<\theta<\dfrac{\pi}{3})$
$\cos 2\theta = \dfrac{-1+\sqrt{33}}{8}$を満たす$\, \theta \,$を$\,\alpha\,$とすると、増減表は下記。
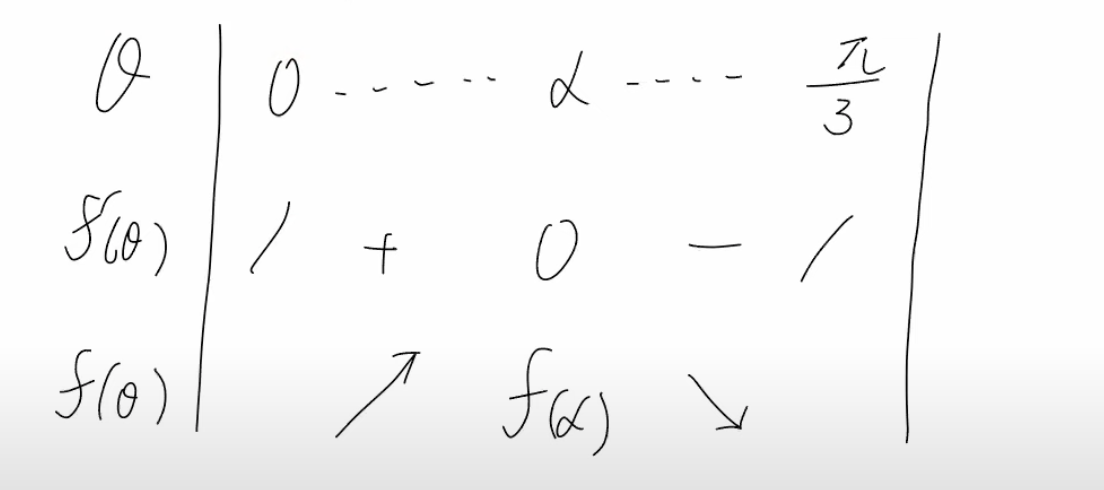
$\therefore \, \theta =\alpha\,$のとき、$f(\theta)\,$は最大となり、$S\,$は最大となる。
$\therefore \,$求める$\cos\angle B\,$は$\dfrac{-1+\sqrt{33}}{8}$
受験勉強・予習復習にはスタサプ
自宅でトップ講師による授業を受けることができるスタサプ。
予備校に通わなくても、スマホで自分のレベルに合わせて授業を受けることができます。
6教科19科目に対応。共通テスト対策講座や志望校別対策講座も全て見放題です。
（僕も数学の学び直しで活用していますが、控えめに言って最高です）
無料体験もあるので、本気で成績を伸ばしたい人はぜひ。
※無料体験はいつ終わるか分からないのでお早めに
さいごに
いかがでしたでしょうか。
今回は2014年京都大学で出題された微分の問題を解説しました。
条件から式を立て、定義域をきちんと考えて落ち着いて解けば解ける問題です。京大を受験した人は落とせない問題だったのではないかと思います。
数学の成績を伸ばしたいと考えている方向けにおすすめの数学の参考書を下記でまとめています。
参考書はとにかく自分に合ったレベルのものを１冊やり切ることがとにかく重要です。
レベルに応じた参考書をやり切る→数学力が向上→レベルに応じた参考書をやり切る→・・・と取り組んでいくことで力がつきます。
参考になれば幸いです。
受験勉強・予習復習にはスタサプ
自宅でトップ講師による授業を受けることができるスタサプ。
予備校に通わなくても、スマホで自分のレベルに合わせて授業を受けることができます。
6教科19科目に対応。共通テスト対策講座や志望校別対策講座も全て見放題です。
（僕も数学の学び直しで活用していますが、控えめに言って最高です）
無料体験もあるので、本気で成績を伸ばしたい人はぜひ。
※無料体験はいつ終わるか分からないのでお早めに
